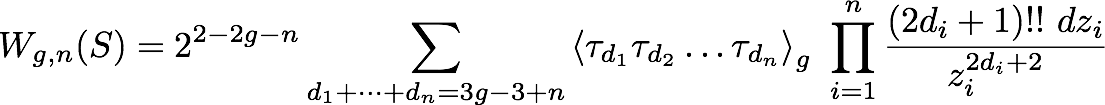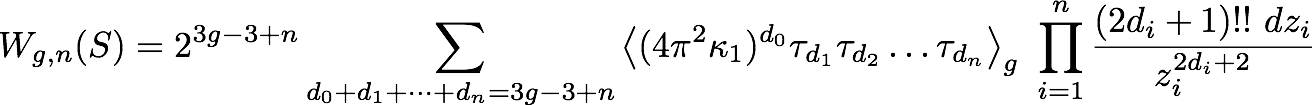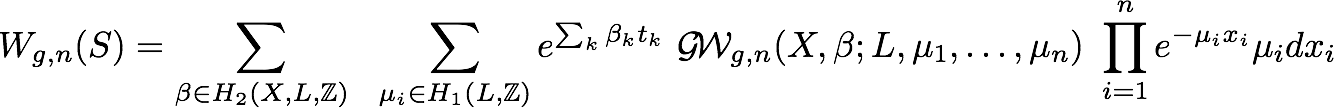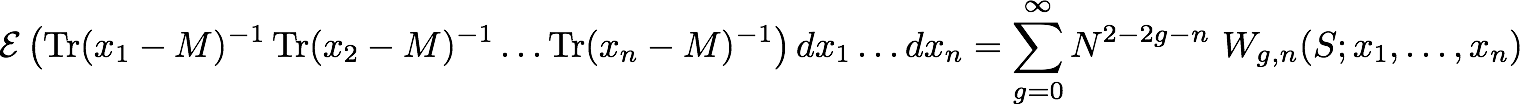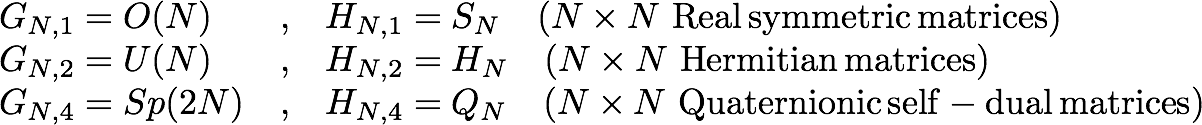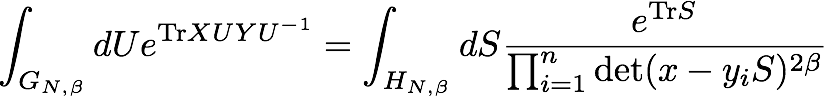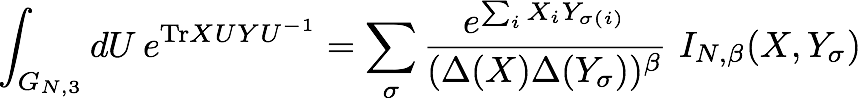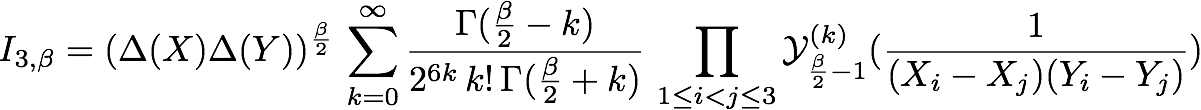in english
in english
In preparation (mid 2017)
-
The topological recursion
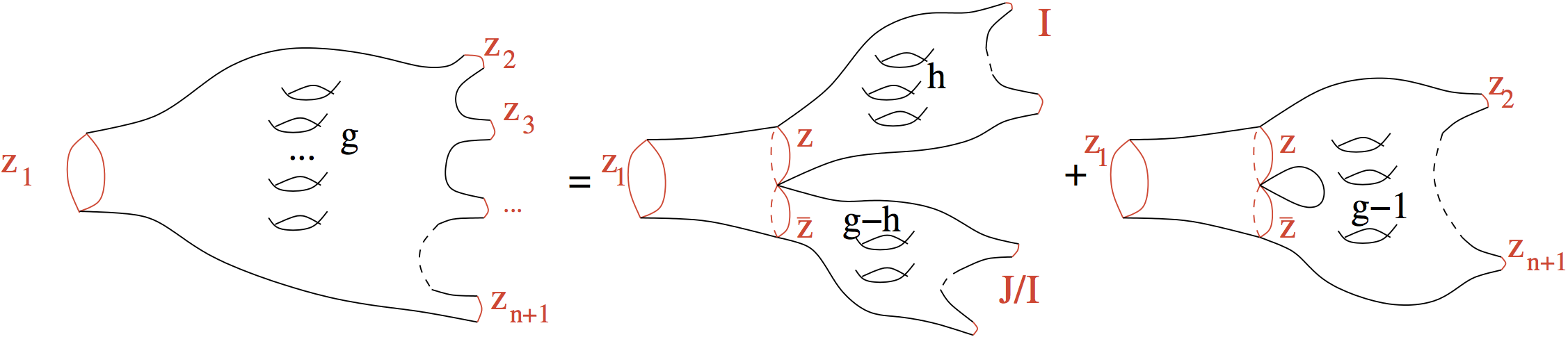
The topological recursion was first discovered in random matrices in 2004 [Eynard04, AMM04].
It became a mathematical theory in 2007 [EO07].
The Topological recursion takes as
input: a spectral curve S (an analytical plane curve with some structure)
and gives
output: a sequence of invariants (the T.R. invariants) of the spectral curve, denoted Wg,n(S). The n=0 invariants are denoted Wg,0(S) = Fg(S).
Fg(S) is a complex number, and Wg,n(S) is a differential n-form.
Some examples:
- The Witten-Kontsevich intersection numbers (curve
\(S : x=y^2\) )
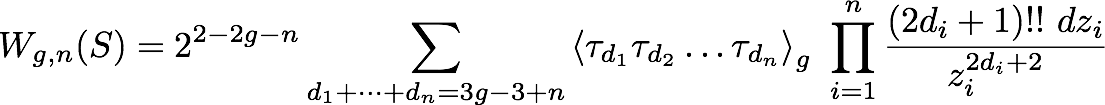
- The Mirzakhani relation among hyperbolic volumes of moduli spaces (curve \( S : y = \sin(\sqrt{x})\) )
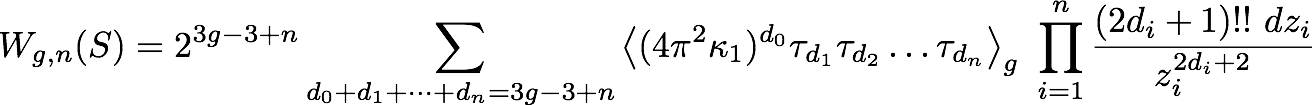
- The Gromov-Witten invariants of toric Calabi-Yau 3-manifolds (curve S: = mirror curve)
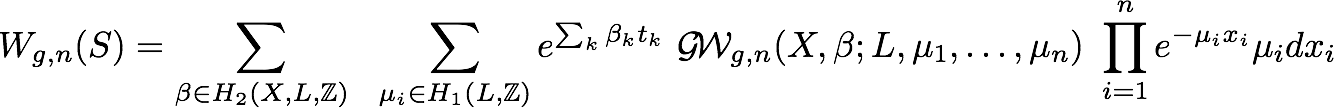
where GWg,n(X,L;�,�) is the open Gromov-Witten invariant of the Calabi-Yau 3-fold X,
i.e. the "number" of holomorphic immersions in X of surfaces of genus
g, with n boundaries, so that boundaries are immersed on a special
Lagrangian submanifold L, with winding number �i, and of relative homology class �.
- the large size expansion of random matrix laws (curve S: = equilibrium spectral density at large N)
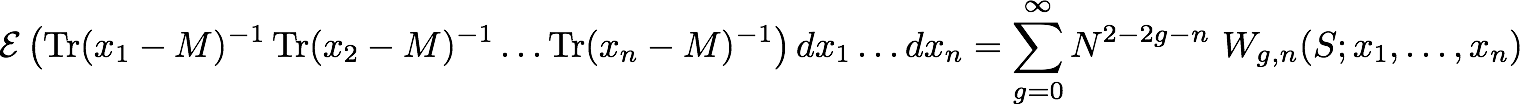
- the enumeration of maps of all topologies (curve S: = counting function of rooted planar maps)
- the WKB asymptotic expansion of Hitchin systems ( curve S: = Hitchin's spectral curve)
- The Knot polynomials (Jones, Homfly,...) ( curve S: = A-polynomial of the knot)
The T.R. invariants have many beautiful mathematical properties:
- symplectic invariance
- modular properties, automorphicity
- form-cycle dualities for their deformations
- nice behavior under limits
- homogeneity
-
Random Matrices
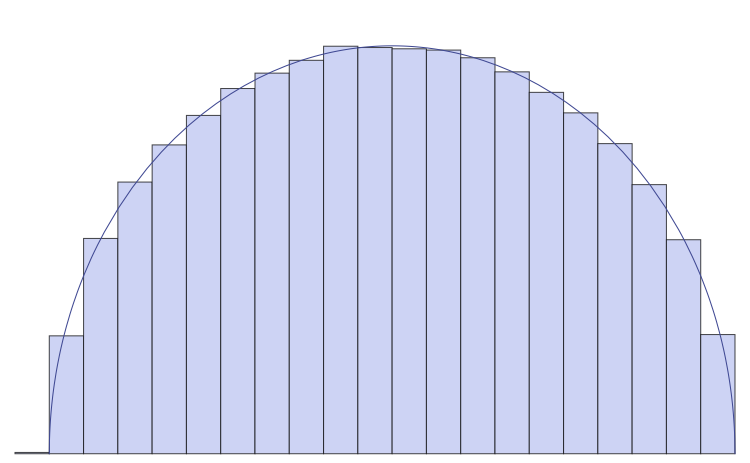
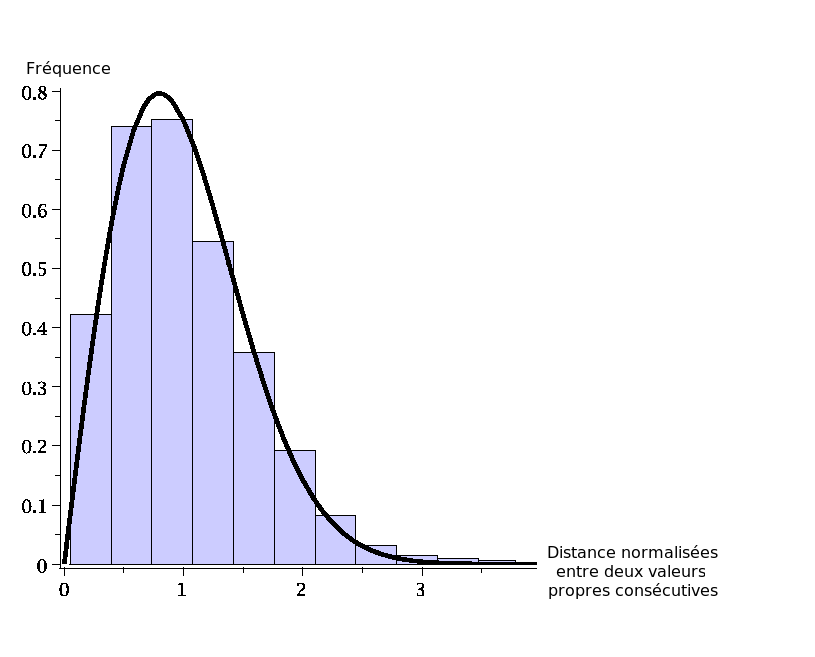
A main question in random matrix theory is the large size asymptotic behavior of the eigenvalues distribution.
Below: plots of histograms for eigenvalues af a randdom Hermitian
matrix, in a Gaussian model (semi-circle law), and non Gaussian. In the
large size (N) limit, the eigenvalue density tends to an algebraic curve. The deviation, of order 1/N2, is also an algebraic function, and more generally, all the coefficients in the 1/N2 expandion are algebraic functions.
- See here : my GOE online generator.
- See here : spectral curve of a quartic matrix model.
of Harish-Chandra- Itzykson-Zuber type.
Let \(G\) be a compact connected semi-simple complex Lie group.
Let \(\text{Weyl}(G)\) its Weyl group.
Let \(\mathfrak g\) its Lie algebra, with \(<,>\) an invariant bilinear form (ex: Killing form).
Let \(\mathfrak U\) its envelopping algebra.
Let \(\mathfrak h\) a Cartan sub-algebra, and Let \(\mathfrak B_+\) its strict Borel algebra,
Let \(X,Y \in \mathfrak h\).
For any \(G\)-invariant polynomial function \(f\in H^0(\mathfrak U\times\mathfrak U,\mathbb C)^G\) of 2 variables,
where \(G\)-invariant means
\[
\forall X,Y\in \mathfrak U, \forall g\in G , \qquad
f(\operatorname{Adj}_g(x),\operatorname{Adj}_g(y)) = f(x,y).\]
I found in [E-PF05] [dFEPFZ] that:
\[
Equation
\]
Example, if we represent \(G\) with matrices,
we choose the invariant bilinear form to be
the trace \( < X,Y>=\operatorname{Tr} X Y\).
The Cartan algebra \(\mathfrak h\) is the set of diagonal matrices,
and the Borel algebra \(\mathfrak B_+\) is the set of strictly upper triangular matrices.
Let X and Y diagonal matrices in the Cartan Algebra of G.
For any polynomial function f(x,y) of 2 variables, I found in [E-PF05] [dFEPFZ] that:
where the product is over positive roots in a dual Cartan
subalgebra, and the last integral is over the strictly positive Borel
subalgebra, and is a Gaussian integral.
(for G=SU(N), the integral is over strictly upper triangular matrices).
The case f=1, is Harish-Chandra formula.
Example of application:
We denote the classical groups by 2 indices \(N\)=size and \(\beta\)=1,2,4:
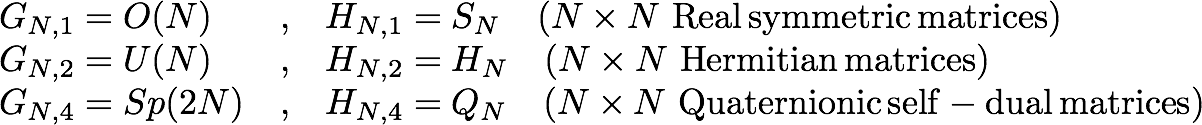
\(H_{N,\beta}\) is the Lie algebra of \(G_{N,\beta}\) are diagonal matrices.
\(X\) and \(Y\) are diagonal matrices.
For \(\beta=2\) it turns out that diagonal matrices are in the Lie algebra, so that it is the same thing as Harish-Chandra, but for other values of \(\beta\) there is at present no known closed formula for all \(N\) and \(\beta\).
However, I found the following:
I found the following results
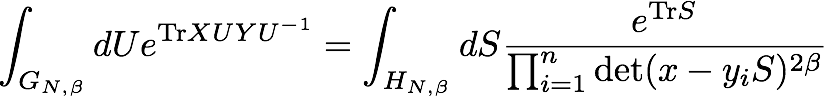

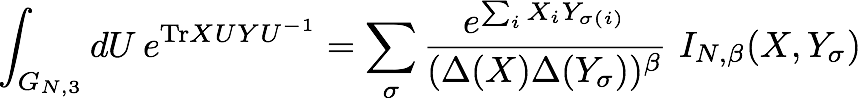
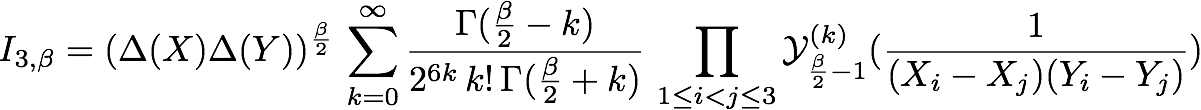
where \(\mathcal Y_n\) is the Bessel Function of the Second Kind, and \(\mathcal Y^{(k)}_n\) is its k-th derivative.

Enumerative geometry
Integrable systems
others
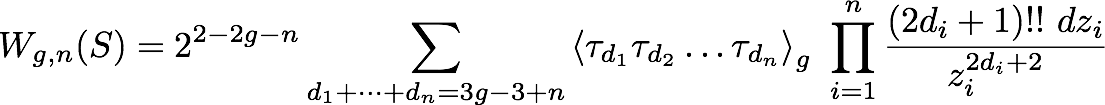
 in english
in english